Pembahasan Soal Ujian Profesi Aktuaris
SOAL
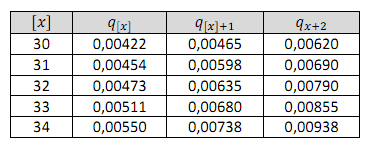
Berikut ini adalah tabel mortalitas select dan ultimate dengan periode seleksi 2 tahun
Hitunglah nilai \(_{2|}{q_{[30] + 1}}\)
- 0.0053
- 0.0058
- 0.0063
- 0.0068
- 0.0073
Pembahasan Ujian PAI: A50 – No. 12 – Mei 2017
with
no comment
Leave A Comment
You must be logged in to post a comment
