Pembahasan Soal Ujian Profesi Aktuaris
SOAL
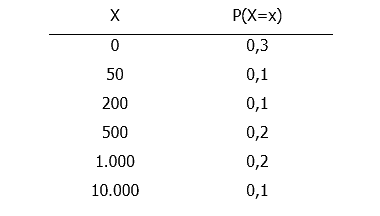
Suatu perusahaan asuransi memodelkan peubah acak klaim, X, untuk polis asuransi tertentu sebagai berikut:
Distribusi besar klaim diatas memiliki parameter sebagai berikut:
q = peluang terjadi klaim tidak nol
B = Distribusi bersyarat atas besar klaim, diberikan terjadi klaim
Cari simpangan baku dari B!
You must be logged in to post a comment
Data Polis adalah perusahaan media yang memberikan informasi mengenai perkembangan industri perasuransian dan manajemen risiko saat ini. Topik yang dibahas dari berbagai sudut pandang agar memperoleh perspektif yang lebih jelas dan lengkap. Hubungi kami melalui email untuk berdiskusi dengan kami: [email protected]
PT Data Teknologi Terintegrasi
MTH Square, GF A4/A
Jl. Letjen M.T. Haryono No. Kav 10, Jakarta Timur 13330
Phone: +62 856 856 0000
©
By Data Polis. All Rights Reserved.
