Pembahasan Soal Ujian Profesi Aktuaris
| Institusi |
: |
Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian |
: |
Metoda Statistika |
| Periode Ujian |
: |
November 2016 |
| Nomor Soal |
: |
12 |
SOAL
Anda mencocokkan model berikut dalam empat pengamatan
\({Y_i} = {\beta _1} + {\beta _2}{X_{2i}} + {\beta _3}{X_{3i}} + {\varepsilon _i},{\rm{ }}i = 1,2,3,4\)
Diberikan data sebagai berikut
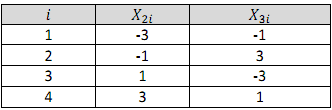
Estimasi least square dari \({\beta _3}\) dinyatakan sebagai \({\widehat \beta _3} = \sum\limits_{i = 1}^4 {{w_i}{Y_i}{\rm{ }}} \), tenteukan nilai dari \(({w_1},{w_2},{w_{3,}}{w_4})\)
- \(( – \frac{1}{{20}},\frac{3}{{20}}, – \frac{3}{{20}},\frac{1}{{20}})\)
- \(( – \frac{1}{{20}}, – \frac{3}{{20}},\frac{3}{{20}},\frac{1}{{20}})\)
- \((\frac{1}{{20}}, – \frac{2}{{20}},\frac{2}{{20}}, – \frac{1}{{20}})\)
- \(( – \frac{1}{{20}},\frac{2}{{20}}, – \frac{2}{{20}},\frac{1}{{20}})\)
- \((\frac{1}{4},\frac{1}{4}, – \frac{1}{4}, – \frac{1}{4})\)
| Diketahui |
\({Y_i} = {\beta _1} + {\beta _2}{X_{2i}} + {\beta _3}{X_{3i}} + {\varepsilon _i},{\rm{ }}i = 1,2,3,4\)

|
| Rumus yang digunakan |
\({\widehat \beta _3} = \sum\limits_{i = 1}^4 {{w_i}{Y_i}{\rm{ }}} = \sum\limits_{i = 1}^4 {\left[ {\frac{{({x_i} – \overline x )}}{{\sum\limits_{i = 1}^n {{{({x_i} – \overline x )}^2}} }}} \right]} {Y_i}\) |
| Proses pengerjaan |
\({w_i} = \left[ {\frac{{({x_i} – \overline x )}}{{\sum\limits_{i = 1}^n {{{({x_i} – \overline x )}^2}} }}} \right],\) dimana
\({\overline x _3} = \frac{{ – 2 + 4 + – 4 + 2}}{4} = 0\) dan
\(\sum\limits_{i = 1}^n {{{({x_i} – \overline x )}^2}} = {( – 2)^2} + {(4)^2} + {( – 4)^2} + {(2)^2} = 40\)
sehingga
\({w_1} = \frac{{ – 2}}{{40}} = \frac{{ – 1}}{{20}}\)
\({w_2} = \frac{4}{{40}} = \frac{2}{{20}}\)
\({w_3} = \frac{{ – 4}}{{40}} = \frac{{ – 2}}{{20}}\)
\({w_4} = \frac{2}{{40}} = \frac{1}{{20}}\) |
| Jawaban |
a. \(( – \frac{1}{{20}},\frac{3}{{20}}, – \frac{3}{{20}},\frac{1}{{20}})\) |









