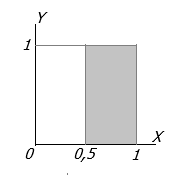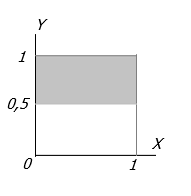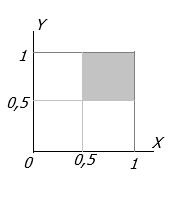| Misalkan | X ialah waktu lamanya komponen 1 sebelum rusak
Y ialah waktu lamanya komponen 2 sebelum rusak
\(P(X\,atau\,Y\, \ge \,0,5)\, = \,P(X \ge 0,5) + P(Y \ge 0,5) – P(X \ge 0,5\,dan\,Y \ge 0,5)\) |
| Step 1 | 
Untuk X>0,5\(P(X > 0,5) = \int\limits_0^1 {\int\limits_{0,5}^1 {(x + y)} } \,dxdy\)
\(P(X > 0,5) = \int\limits_0^1 {\left( {\frac{{1 – 0,{5^2}}}{2} + y(1 – 0,5)} \right)dy} \)
\(P(X > 0,5) = \int\limits_0^1 {\left( {\frac{3}{8} + \frac{1}{2}y} \right)} dy\)
\(P(X > 0,5) = \left( {\frac{3}{8} + \frac{1}{2}\frac{1}{2}} \right)\)
\(P(X > 0,5) = \frac{5}{8}\)
Untuk Y>0,5
\(P(Y > 0,5) = \int\limits_0^1 {\int\limits_{0,5}^1 {(x + y)} } \,dydx\)
\(P(Y > 0,5) = \int\limits_0^1 {\left( {(1 – 0,5)x + \frac{{1 – 0,{5^2}}}{2}} \right)dx} \)
\(P(Y > 0,5) = \int\limits_0^1 {\left( {\frac{1}{2}x + \frac{3}{8}} \right)} dx\)
\(P(Y > 0,5) = \left( {\frac{1}{2}\frac{1}{2} + \frac{3}{8}} \right)\)
\(P(Y > 0,5) = \frac{5}{8}\) 
Untuk X>0,5 dan Y>0,5
\(P(X > 0,5 \cap Y > 0,5) = \int\limits_{0,5}^1 {\int\limits_{0,5}^1 {(x + y)\,dxdy} } \)
\(P(X > 0,5 \cap Y > 0,5) = \int\limits_{0,5}^1 {\left( {\frac{1}{2}y + \frac{{1 – 0,{5^2}}}{2}} \right)dy} \)
\(P(X > 0,5 \cap Y > 0,5) = \int\limits_{0,5}^1 {\left( {\frac{1}{2}y + \frac{3}{8}} \right)dy} \)
\(P(X > 0,5 \cap Y > 0,5) = \frac{1}{2}\left( {\frac{{1 – 0,{5^2}}}{2}} \right) + \frac{3}{8}\frac{1}{2}\)
\(P(X > 0,5 \cap Y > 0,5) = \frac{1}{2}\frac{3}{8} + \frac{3}{8}\frac{1}{2}\)
\(P(X > 0,5 \cap Y > 0,5) = \frac{3}{8}\)
|
| Step 2 | \(P(X\,atau\,Y\, \ge \,0,5)\, = \,\frac{5}{8} + \frac{5}{8} – \frac{3}{8}\)
\(P(X\,atau\,Y\, \ge \,0,5)\, = \,\frac{7}{8}\) |