Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Pemodelan dan Teori Risiko |
| Periode Ujian | : | November 2018 |
| Nomor Soal | : | 22 |
SOAL
Diberikan grafik fungsi kepadatan untuk suatu kerugian sebagai berikut:
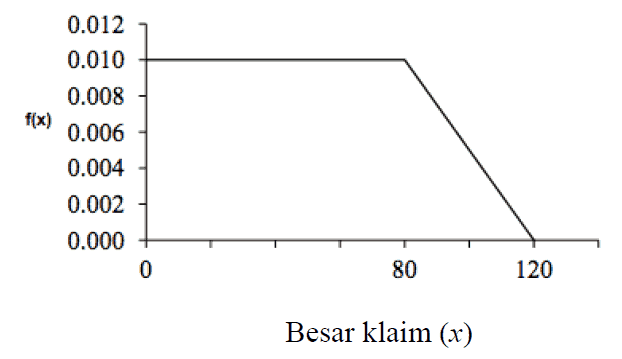
Hitung “loss elimination ratio” dari suatu ordinary deductible sebesar 20
- 0,210
- 0,650
- 0,015
- 0,150
- 0,355
| Diketahui | Diberikan grafik fungsi kepadatan untuk suatu kerugian sebagai berikut:
|
| Rumus yang digunakan | \(\begin{array}{*{20}{c}} {E\left[ X \right] = \int\limits_{ – \infty }^\infty {xf\left( x \right)dx} ,}&{E\left[ {X \wedge u} \right] = \int\limits_0^u {xf\left( x \right)dx} + 20 \cdot \left[ {1 – F\left( x \right)} \right]} \end{array}\) \(LER = \frac{{E\left[ {X \wedge u} \right]}}{{E\left[ X \right]}}\) |
| Proses pengerjaan | Dari Gambar dapat dilihat 0.01 konstan dari 0 sampai 80 dan kemudian menurun sebesar \(– \frac{{0.01}}{{40}}\) dan sama dengan 0 pada 120 sehingga diperoleh model distribusi \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.01,}&{0 \le x \le 80} \end{array}}\\ {\begin{array}{*{20}{c}} {\frac{{0.01\left( {120 – x} \right)}}{{40}},}&{80 < x \le 120} \end{array}} \end{array}} \right.\) |
| \(E\left[ X \right] = \int\limits_0^{120} {xf\left( x \right)dx} = \int\limits_0^{80} {0.01xdx} + \int\limits_{80}^{120} {\left( {0.01} \right)\left( {\frac{{120 – x}}{{40}}} \right)xdx} \) \(E\left[ X \right] = 0.01\left( {\frac{{{{80}^2}}}{2}} \right) + \frac{{0.01}}{{40}}\int\limits_{80}^{120} {\left( {120x – {x^2}} \right)dx} \) \(E\left[ X \right] = 32 + \frac{1}{{4000}}\left. {\left( {60{x^2} – \frac{{{x^3}}}{3}} \right)} \right|_{80}^{120} = 50\frac{2}{3}\) | |
| \(E\left[ {X \wedge 20} \right] = \int\limits_0^{20} {xf\left( x \right)dx} + 20 \cdot \left[ {1 – F\left( {20} \right)} \right] = \int\limits_0^{20} {xf\left( x \right)dx} + 20 \cdot \left[ {1 – \int\limits_0^{20} {f\left( x \right)dx} } \right]\) \(E\left[ {X \wedge 20} \right] = \int\limits_0^{20} {0.01xdx} + 20 \cdot \left[ {1 – \int\limits_0^{20} {0.01dx} } \right]\) \(E\left[ {X \wedge 20} \right] = 0.01\left( {\frac{{{{20}^2}}}{2}} \right) + 20\left[ {1 – 0.01\left( {20} \right)} \right] = 18\) | |
| \(LER = \frac{{E\left[ {X \wedge 20} \right]}}{{E\left[ X \right]}} = \frac{{18}}{{50.66667}} = 0.35526\) | |
| Jawaban | e. 0,355 |


