Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Permodelan dan Teori Risiko |
| Periode Ujian | : | Juni 2016 |
| Nomor Soal | : | 19 |
SOAL
Banyaknya klaim dari sebuah pertanggungan asuransi adalah sebagai berikut:
| Banyaknya klaim (number of claims) | Jumlah Polis (number of policies) |
| 0 | 325 |
| 1 | 325 |
| 2 | 225 |
| 3 | 100 |
| 4 | 25 |
| 5+ | 0 |
Sebuah distibusi Poisson dengan rata-rata (mean) 1,2 disesuaikan (fitted) dengan data. Hitunglah nilai dari statistik Chi-Square.
- kurang dari 9
- paling sedikit 9, akan tetapi kurang dari 11
- paling sedikit 11, akan tetapi kurang dari 13
- paling sedikit 13, akan tetapi kurang dari 15
- lebih dari 15
| Diketahui | | Banyaknya klaim (number of claims) | Jumlah Polis (number of policies) | | 0 | 325 | | 1 | 325 | | 2 | 225 | | 3 | 100 | | 4 | 25 | | 5+ | 0 |
Sebuah distibusi Poisson dengan rata-rata (mean) 1,2 disesuaikan (fitted) dengan data |
| Rumus yang digunakan | nilai dari statistik Chi-Square: \(\sum {\frac{{{{\left( {{n_i} – n{p_i}} \right)}^2}}}{{n{p_i}}}} \) |
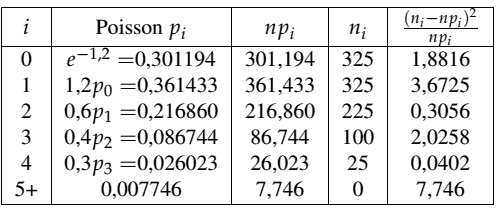
| Proses pengerjaan | Pada soal ini harus tetap memperhitungkan grup yang akan memiliki klaim 5 dan lebih dari 5.
Pada tabel berikut, aturan untuk kelas (a, b, 0) digunakan untuk menghitung peluang Poisson \({p_i}\) dan \({p_5} = 1 – \sum\limits_{i = 0}^4 {{p_i}} \)
\(\sum {\frac{{{{\left( {{n_i} – n{p_i}} \right)}^2}}}{{n{p_i}}}} = 15,6714\) |
| Jawaban | E. lebih dari 15 |