Pembahasan Ujian PAI: A60 – No. 4 – Mei 2018

Pembahasan Soal Ujian Profesi Aktuaris

Institusi	:	Persatuan Aktuaris Indonesia (PAI)
Mata Ujian	:	Matematika Aktuaria
Periode Ujian	:	Mei 2018
Nomor Soal	:	4

SOAL

Untuk (x) dan (y) yang saling bebas dengan \({q_x} = 0,2\) dan \({q_y} = 0,1\). Diketahui bahwa tingkat mortalitas untuk integral ages mengikuti distribusi seragam.

 

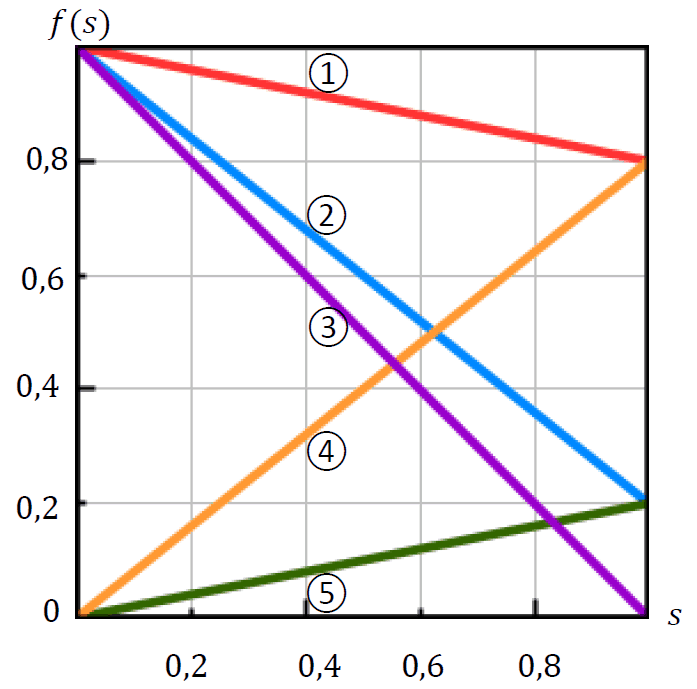
Manakah grafik yang tepat untuk menggambarkan \({}_s{p_x}\) sebagai fungsi dari \(s\) dengan \(0 \le s \le 1\)?

1. 1
2. 2
3. 3
4. 4
5. 5

[showhide type more_text=”Kunci Jawaban & Pembahasan” less_text=”Sembunyikan Kunci Jawaban & Pembahasan”]

Diketahui	Untuk (x) dan (y) yang saling bebas dengan \({q_x} = 0,2\) dan \({q_y} = 0,1\). Diketahui bahwa tingkat mortalitas untuk integral ages mengikuti distribusi seragam.
Rumus yang digunakan	Integral ages mengikuti distribusi seragam \({}_s{p_x} = s \cdot {p_x}\), \({}_s{q_x} = 1 – s \cdot {p_x}\)
Proses pengerjaan	Diketahui bahwa tingkat mortalitas untuk integral ages mengikuti distribusi seragam, maka \({}_s{p_x} = s \cdot {p_x}\), sehingga \({}_s{p_x} = 1 – s \cdot {q_x} = 1 – 0.2s\). Maka grafik yang tepat adalah grafik nomor 1
Jawaban	a. 1

[/showhide]