Pembahasan Soal Ujian Profesi Aktuaris
| Institusi |
: |
Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian |
: |
Metoda Statistika |
| Periode Ujian |
: |
November 2016 |
| Nomor Soal |
: |
11 |
SOAL
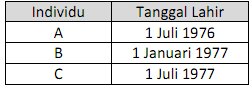
Dari studi mortalita yang diobservasi pada tahun kalender 2007, diperoleh data sebagi berikut:
Dalam periode observasi tersebut, hanya individu B yang meninggal dunia dan tidak ada individu yang melakukan withdrawal. Dengan menggunakan metode exact exposure (asumsi force of mortality adalah konstan) diperoleh \({\widehat q_{30}} = 0.451\). Pada tanggal berapa individu B meninggal dunia?
- 1 Agustus 2007
- 1 September 2007
- 1 Oktober 2007
- 1 November 2007
- 1 Juli 2007
| Diketahui |
Observasi tahun 2007
Metode exact exposure \({\widehat q_{30}} = 0.451\) |
| Rumus yang digunakan |
\({y_i} = \) tanggal awal pengamatan – tanggal lahir
\({z_i} = \) tanggal akhir pengematan – tanggal lahir
\({\theta _{}}{\rm{ = }}\) tanggal meninggal – tanggal lahir
\({\phi _i}{\rm{ = }}\) tanggal withdrawal – tanggal lahir
\({r_i} = \left\{ \begin{array}{l} 0\\ {y_i} – x \end{array} \right.\begin{array}{*{20}{c}} {,jika\_{y_i} \le x{\rm{ }}}\\ {,jika\_x < {y_i} < x + 1} \end{array}\)
\({s_i} = \left\{ \begin{array}{l} {z_i} – x\\ 1 \end{array} \right.\begin{array}{*{20}{c}} {,jika\_x < {z_i} < x + 1}\\ {,jika\_{z_i} \ge x + 1{\rm{ }}} \end{array}\)
\({l_i} = \left\{ \begin{array}{l} 0\\ {\theta _i} – x\\ 0 \end{array} \right.\begin{array}{*{20}{c}} \begin{array}{l} ,jika\_{\theta _i} = 0\\ ,jika\_x < {\theta _i} < x + 1 \end{array}\\ {,jika\_{\theta _i} \ge x + 1{\rm{ }}} \end{array}\)
\({k_i} = \left\{ \begin{array}{l} 0\\ {\phi _i} – x\\ 0 \end{array} \right.\begin{array}{ {20}{c}} \begin{array}{l} ,jika\_{\phi _i} = 0\\ ,jika\_x < {\phi _i} < x + 1 \end{array}\\ {,jika\_{\phi _i} \ge x + 1{\rm{ }}} \end{array}\)
\({\varepsilon _{eksak}} = \left\{ \begin{array}{l} {s_i} – {r_i}\\ {k_i} – {r_i}\\ {l_i} – {r_i} \end{array} \right.\begin{array}{*{20}{c}} \begin{array}{l} ,jika\_seseorang\_tidak\_meninggal\_dan\_withdraw\\ ,jika\_seseorang\_withdraw \end{array}\\ {,jika\_seseorang\_meninggal{\rm{ }}} \end{array}\) |
| Proses pengerjaan |
| Tgl Lahir |
\({y_i}\) |
\({z_i}\) |
\({\theta _i}\) |
\({\phi _i}\) |
\({r_i}\) |
\({s_i}\) |
\({l_i}\) |
\({k_i}\) |
Eksposur eksak |
| 1 Jul 76 |
30.5 |
31.5 |
0 |
0 |
0.5 |
1 |
0 |
0 |
0.5 |
| 1 Jan 77 |
30 |
31 |
30+x |
0 |
0 |
1 |
x |
0 |
X |
| 1 Jul 77 |
29.50 |
30.5 |
0 |
0 |
0 |
0.5 |
0 |
0 |
0.5 |
| TOTAL |
1+x |
\({\widehat q_{30}} = 1 – \exp ( – \frac{1}{{1 + x}})\)
\(\Leftrightarrow 0.451 = 1 – \exp ( – \frac{1}{{1 + x}})\)
\(\Leftrightarrow \exp ( – \frac{1}{{1 + x}}) = 0.549\)
\(\Leftrightarrow – \frac{1}{{1 + x}} = \ln (0.549)\)
\(\Leftrightarrow \frac{1}{{1 + x}} = 0.59966\)
\(\Leftrightarrow x = 0.66762\)
selanjutnya
\(\frac{b}{{12}} = 0.66762\)
\(\Leftrightarrow b = 8.011445\)
Sehingga, jika 30+0.0 dimulai 1 januari 2007 (bulan ke-1) maka individu B meninggal dunia sekita tanggal 1 September 2007 |
| Jawaban |
a. 1 September 2007 |
