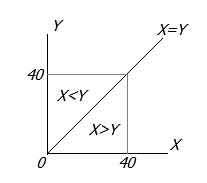Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | A20 – Probabilitas dan Statistika |
| Periode Ujian | : | Juni 2016 |
| Nomor Soal | : | 11 |
SOAL
Misalkan waktu harapan hidup satu pasangan suami istri adalah saling bebas dan berdistribusi uniform pada interval [0, 40]. Sebuah perusahaan asuransi menawarkan dua produk asuransi pada pasangan yang sudah menikah yaitu sbb:
- Produk 1 : Pembayaran benefit ketika suami dari pasangan tersebut meninggal dunia
- Produk 2 : Pembayaran benefit ketika baik suami dan istri dari pasangan tersebut meninggal dunia
Berapa kovariansi dari waktu pembayaran dari dua produk di atas?
- 0
- 44,4
- 66,7
- 200,0
- 466,7
PEMBAHASAN
| Misalkan | X ialah suami meninggal
Y ialah istri meninggal
Z ialah suami dan istri meninggal
X ~ Uniform [0,40]
Y ~ Uniform [0,40] |
| Step 1 | \(E[X] = \int\limits_0^{40} {x\left( {\frac{1}{{40}}} \right)} dx\)
\(E[X] = \frac{1}{{40}}\left( {\frac{{{{40}^2}}}{2}} \right)\)
\(E[X] = 20\) |
| Step 2 | Z ~ Max(X,Y)
\(f(z) = n\,{[{F_X}(z)]^{n – 1}}\,{f_X}(z)\)
\(f(z) = 2{\left( {\frac{z}{{40}}} \right)^{2 – 1}}\left( {\frac{1}{{40}}} \right)\)
\(f(z) = \frac{z}{{800}}\)
\(E[Z] = \int\limits_0^{40} {z\left( {\frac{z}{{800}}} \right)} dz\)
\(E[Z] = \frac{1}{{800}}\left( {\frac{{{{40}^3}}}{3}} \right)\)
\(E[Z] = 26,667\)
|
| Step 3 | \(f(x,y) = f(x)f(y)\)
\(f(x,y) = \frac{1}{{40}}\frac{1}{{40}}\)
\(f(x,y) = \frac{1}{{1600}}\) |
| Step 4 | \(Z = \left\{ \begin{array}{l}X\,\,\,\,\,\,\,Y < X\\Y\,\,\,\,\,\,\,\,X < Y\end{array} \right.\) 
Untuk X > Y
\(E[XZ] = \int\limits_0^{40} {\int\limits_0^x {xx\,\frac{1}{{1600}}dy\,dx} } \)
\(E[XZ] = \frac{1}{{1600}}\int\limits_0^{40} {{x^3}\,dx} \)
\(E[XZ] = \frac{1}{{1600}}\left( {\frac{{{{40}^4}}}{4}} \right)\)
\(E[XZ] = 400\)
Untuk X < Y
\(E[XZ] = \int\limits_0^{40} {\int\limits_0^y {xy\frac{1}{{1600}}dx\,dy} } \)
\(E[XZ] = \frac{1}{{1600}}\int\limits_0^{40} {\frac{{{y^3}}}{2}dy} \)
\(E[XZ] = \frac{1}{{1600}}\frac{{{{40}^4}}}{8}\)
\(E[XZ] = 200\)
|
| Step 5 | E[XZ] = 400+200 E[XZ]=600 |
| Step 6 | \(Cov[X,Z] = E[XZ] – E[X]E[Z]\)
\(Cov[X,Z] = 600 – (20)(26,667)\)
\(Cov[X,Z] = 66,66\)
\(Cov[X,Z] = 66,7\) |
| Jawaban | c. 66,7 |