Pembahasan Soal Ujian Profesi Aktuaris
SOAL
Keluarga Joko membeli dua polis dari perusahaan asuransi yang sama. Kerugian atas dua polis tersebut saling bebas dan memiliki distribusi kontinyu seragam pada interval 0 sampai 10. Satu polis memiliki deductible 1, dan yang satunya memiliki deductible 2. Keluarga Joko mengalami tepat satu kerugian dari masing-masing polis. Hitung peluang total manfaat yang dibayarkan ke Keluarga Joko tidak melebihi 5!
You must be logged in to post a comment
Data Polis adalah perusahaan media yang memberikan informasi mengenai perkembangan industri perasuransian dan manajemen risiko saat ini. Topik yang dibahas dari berbagai sudut pandang agar memperoleh perspektif yang lebih jelas dan lengkap. Hubungi kami melalui email untuk berdiskusi dengan kami: [email protected]
PT Data Teknologi Terintegrasi
MTH Square, GF A4/A
Jl. Letjen M.T. Haryono No. Kav 10, Jakarta Timur 13330
Phone: +62 856 856 0000
©
By Data Polis. All Rights Reserved.
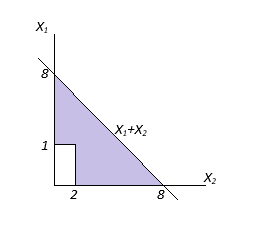\({x_1} > 1,{x_2} > 2\)
\({Y_1} + {Y_2} \le 5 = {x_1} + {x_2} – 3 \le 5\)
\({Y_1} + {Y_2} \le 5 = {x_1} + {x_2} \le 8\)