Pembahasan Soal Ujian Profesi Aktuaris
Institusi
:
Persatuan Aktuaris Indonesia (PAI)
Mata Ujian
:
Metoda Statistika
Periode Ujian
:
Mei 2017
Nomor Soal
:
7
SOAL
Dalam suatu tabel double decrement, diberikan data sebagi berikut:
20
25
30
35
40
Diketahui
Rumus yang digunakan
\(_tq_x^{(j)} = \frac{{_td_x^{(j)}}}{{l_x^{(\tau )}}}\)
\(_tq_x^{(\tau )} = \sum\limits_{j = 1}^m {q_x^{(j)}} \)
\(q_x^{(\tau )} = \frac{{l_x^{(\tau )} – l_{x + 1}^{(\tau )}}}{{l_x^{(\tau )}}}\)
Proses pengerjaan
\(d_{26}^{(1)} = l_{26}^{(\tau )}.q_{26}^{(1)}\)
\(= 8400{\rm{ }}{\rm{. }}(0.02)\)
\(= 168\)
\(d_{26}^{(2)} = l_{26}^{(\tau )}.q_{26}^{(2)}\)
\(= 8400{\rm{ }}{\rm{. }}(0.15)\)
\(= 1260\)
\(q_{25}^{(\tau )} = q_{25}^{(1)} + q_{25}^{(2)} = 0.01 + 0.15 = 0.16\)
\(q_{25}^{(\tau )} = \frac{{l_{25}^{(\tau )} – l_{26}^{(\tau )}}}{{l_{25}^{(\tau )}}}\)
\(\Leftrightarrow 0.16 = \frac{{l_{25}^{(\tau )} – 8400}}{{l_{25}^{(\tau )}}}\)
\(\Leftrightarrow l_{25}^{(\tau )} – 0.16{\rm{ }}l_{25}^{(\tau )} = 8400\)
\(\Leftrightarrow {\rm{ }}l_{25}^{(\tau )} = \frac{{8400}}{{0.84}}\)
\(\Leftrightarrow {\rm{ }}l_{25}^{(\tau )} = 10000\)
bila \(q_{25}^{(2)}\) menjadi \(0.3\)
\(q_{25}^{(\tau )} = \sum\limits_{j = 1}^m {q_{25}^{(j)} = 0.01 + 0.3 = 0.31} \)
\(q_{25}^{(\tau )} = \frac{{10000 – l_{26}^{(\tau )}}}{{10000}}\)
\(\Leftrightarrow 0.31 = \frac{{10000 – l_{26}^{(\tau )}}}{{10000}}\)
\(\Leftrightarrow l_{26}^{(\tau )} = 6900\)
\(d_{26}^{(1)} = l_{26}^{(\tau )}.q_{26}^{(1)}\)
\(= 6900{\rm{ (0}}{\rm{.02)}}\)
\({\rm{ = 138}}\)
selisih
Jawaban c. 30
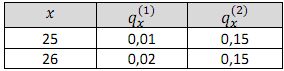Bila diketahui \(l_{26}^{(T)} = 8400,\) hitunglah perubahan pada \(d_{26}^{(1)}\) jika \({\rm{ }}q_{25}^{(2)}\) berubah dari \({\rm{0}}{\rm{.15}}\) menjadi \({\rm{0}}{\rm{.3}}\)