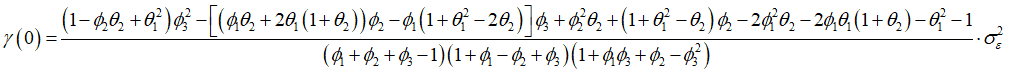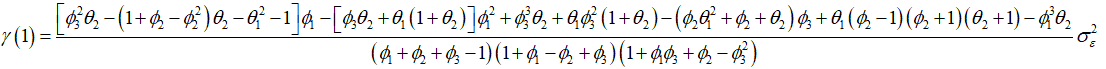Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Metoda Statistika |
| Periode Ujian | : | April 2019 |
| Nomor Soal | : | 7 |
SOAL
Diberikan sebuah persamaan dalam proses ARMA (3,2) sebagai berikut
\({y_t} = 0,5{y_{t – 1}} + 0,3{y_{t – 2}} + 0,2{y_{t – 3}} + 4,2 + {\varepsilon _t} – 0,4{\varepsilon _{t – 1}} + 0,1{\varepsilon _{t – 2}}\)
Jika diberikan nilai \(\sigma _\varepsilon ^2 = 1,25\), hitunglah \({\gamma _0}\) dan \({\rho _1}\)
- \({\gamma _0} = 1,267\) dan \({\rho _1} = 0,133\)
- \({\gamma _0} = 1,131\) dan \({\rho _1} = 0,105\)
- \({\gamma _0} = 1,267\) dan \({\rho _1} = 0,105\)
- \({\gamma _0} = 1,131\) dan \({\rho _1} = 0,133\)
- \({\gamma _0} = 1,131\) dan \({\rho _1} = 0,119\)
| Diketahui | ARMA (3,2) dengan model
\({y_t} = 0,5{y_{t – 1}} + 0,3{y_{t – 2}} + 0,2{y_{t – 3}} + 4,2 + {\varepsilon _t} – 0,4{\varepsilon _{t – 1}} + 0,1{\varepsilon _{t – 2}}\) dengan \(\sigma _\varepsilon ^2 = 1,25\)
Dengan bentuk umum \({y_t} = {\phi _1}{y_{t – 1}} + {\phi _2}{y_{t – 2}} + {\phi _3}{y_{t – 3}} + \delta + {\varepsilon _t} + {\theta _1}{\varepsilon _{t – 1}} + {\theta _2}{\varepsilon _{t – 2}}\) |
| Rumus yang digunakan | Rumus Umum Varians dan Kovarians Model ARMA (p,q)
\({y_t} = {\phi _1}{y_{t – 1}} + {\phi _2}{y_{t – 2}} + {\phi _3}{y_{t – 3}} + \delta + {\varepsilon _t} + {\theta _1}{\varepsilon _{t – 1}} + {\theta _2}{\varepsilon _{t – 2}}\)
\(\rho \left( k \right) = \frac{{\gamma \left( k \right)}}{{\gamma \left( 0 \right)}}\) dan \(\gamma \left( i \right) = \sum\limits_{j = 1}^p {{\phi _j}} \gamma \left( {\left| {\tau – i} \right|} \right) + {\sigma ^2}\sum\limits_{k = i}^q {{\theta _j}{\psi _{j – i}}} \) dengan \({\psi _j} = \phi _1^{j – 1}\left( {{\phi _1} + {\theta _1}} \right)\)
Sumber: http://www.maths.qmul.ac.uk/~bb/TimeSeries/TS_Chapter6_2_1.pdf |
| Proses pengerjaan | Dari rumus umum Varians dan Kovarians Model ARMA (3,2) diperoleh
\(\gamma \left( 0 \right) = {\phi _1}\gamma \left( 1 \right) + {\phi _2}\gamma \left( 2 \right) + {\phi _3}\gamma \left( 3 \right) + \sigma _\varepsilon ^2 + {\theta _1}\left( {{\phi _1} + {\theta _1}} \right)\sigma _\varepsilon ^2 + {\theta _2}{\phi _1}\left( {{\phi _1} + {\theta _1}} \right)\sigma _\varepsilon ^2\)
\(\gamma \left( 1 \right) = {\phi _1}\gamma \left( 0 \right) + {\phi _2}\gamma \left( 1 \right) + {\phi _3}\gamma \left( 2 \right) + {\theta _1}\sigma _\varepsilon ^2 + {\theta _2}\left( {{\phi _1} + {\theta _1}} \right)\sigma _\varepsilon ^2\)
\(\gamma \left( 2 \right) = {\phi _1}\gamma \left( 1 \right) + {\phi _2}\gamma \left( 0 \right) + {\phi _3}\gamma \left( 1 \right) + {\theta _2}\sigma _\varepsilon ^2\)
\(\gamma \left( 3 \right) = {\phi _1}\gamma \left( 2 \right) + {\phi _2}\gamma \left( 1 \right) + {\phi _3}\gamma \left( 0 \right)\)
Kemudian lakukan proses substitusi diperoleh
 
Karena nilai penyebut
\(\left( {{\phi _1} + {\phi _2} + {\phi _3} – 1} \right)\left( {1 + {\phi _1} – {\phi _2} + {\phi _3}} \right)\left( {1 + {\phi _1}{\phi _3} + {\phi _2} – \phi _3^2} \right)\)
\(= \left( {0,5 + 0,3 + 0,2 – 1} \right)\left( {1 + 0,5 – 0,3 + 0,2} \right)\left( {1 + 0,5 \cdot 0,2 + 0,3 – {{0,2}^2}} \right)\)
\(= \left( 0 \right)\left( {1,4} \right)\left( {1,36} \right)\)
\(= 0\)
Maka tidak ada jawaban yang tepat. |
| Jawaban | Anulir |