Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Metoda Statistika |
| Periode Ujian | : | November 2016 |
| Nomor Soal | : | 25 |
SOAL
Untuk sebuah deret waktu
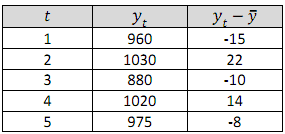
Hitunglah estimasi fungsi autokorelasi oarsial pada time displacement k=2
- -0.14
- -0.63
- 0.22
- 0.28
- 0.36
| Diketahui |  |
| Rumus yang digunakan | autocorrelation \({r_k} = \frac{{\sum\limits_{i = 1}^{n – k} {(y_t^{} – \overline y )(y_{i + k}^{} – \overline y )} }}{{\sum\limits_{i = 1}^n {{{(y_t^{} – \overline y )}^2}} }}\) partial autocorrelation |
| Proses pengerjaan | \({r_1} = \frac{{\sum\limits_{i = 1}^4 {(y_t^{} – \overline y )(y_{i + k}^{} – \overline y )} }}{{\sum\limits_{i = 1}^5 {{{(y_t^{} – \overline y )}^2}} }}\)
\(= \frac{{( – 15)(22) + (22)( – 10) + ( – 10)(14) + (14)( – 8)}}{{{{( – 15)}^2} + {{(22)}^2} + {{( – 10)}^2} + {{(14)}^2} + {{( – 8)}^2}}}\)
\(= – 0.75023\)
\({r_2} = \frac{{\sum\limits_{i = 1}^3 {(y_t^{} – \overline y )(y_{i + k}^{} – \overline y )} }}{{\sum\limits_{i = 1}^5 {{{(y_t^{} – \overline y )}^2}} }}\)
\(= \frac{{( – 15)( – 10) + (22)(14) + ( – 10)( – 8)}}{{{{( – 15)}^2} + {{(22)}^2} + {{( – 10)}^2} + {{(14)}^2} + {{( – 8)}^2}}}\)
\(= 0.503274\) sehingga, \({\widehat \varphi _{22}} = \frac{{(0.503274) – ( – 0.75023)_{}^2}}{{1 – ( – 0.75023)_{_{}}^2}}\) \(= – 0.13628\) \(= – 0.14\) |
| Jawaban | a. -0.14 |


