strong>Pembahasan Soal Ujian Profesi Aktuaris
SOAL
Misalkan seorang mahasiswa yang pergi kuliah antara pukul 8 pagi hingga 08.30 pagi, membutuhkan antara 40 dan 50 menit untuk sampai ke kampus. Misalkan X menyatakan waktu keberangkatan dan Y menyatakan lamanya waktu perjalanan. Jika diasumsikan bahwa peubah acak ini adalah saling bebas dan berdistribusi uniform, hitung peluang bahwa mahasiswa tersebut akan sampai di kampus sebelum pukul 9 pagi!
Data Polis adalah perusahaan media yang memberikan informasi mengenai perkembangan industri perasuransian dan manajemen risiko saat ini. Topik yang dibahas dari berbagai sudut pandang agar memperoleh perspektif yang lebih jelas dan lengkap. Hubungi kami melalui email untuk berdiskusi dengan kami: [email protected]
Marketing Office –
PT Data Teknologi Terintegrasi
MTH Square, GF A4/A
Jl. Letjen M.T. Haryono No. Kav 10, Jakarta Timur 13330
Phone: +62 856 856 0000
Follow Us
©
By Data Polis. All Rights Reserved.
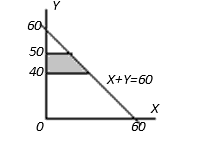\(P(X + Y < 60) = \int\limits_{40}^{50} {\int\limits_0^{60 – y} {f(x)\,f(y)\,dxdy} } \)
\(P(X + Y < 60) = \int\limits_{40}^{50} {\int\limits_0^{60 – y} {\frac{1}{{30}}\frac{1}{{10}}\,\,dxdy} } \)
\(P(X + Y < 60) = \frac{1}{{300}}\int\limits_{40}^{50} {\left( {60 – y – 0} \right)\,dy\,} \)
\(P(X + Y < 60) = \frac{1}{{300}}\left( {60(50 – 40) – \frac{1}{2}({{50}^2} – {{40}^2})} \right)\)
\(P(X + Y < 60) = \frac{1}{{300}}\left( {600 – 450} \right)\)
\(P(X + Y < 60) = \frac{1}{2}\)
