Pembahasan Soal Ujian Profesi Aktuaris
Institusi : Persatuan Aktuaris Indonesia (PAI) Mata Ujian : A20 – Probabilitas dan Statistika Periode Ujian : Maret 2016 Nomor Soal : 22
SOAL
Misalkan \({X_1},{X_2},{X_3}\) ialah peubah acak yang identik dan saling bebas yang mana memiliki fungsi kepadatan peluang \(f(x) = \exp ( – x),\,0 < x < \infty \,\) dan \(f(x) = 0\,untuk\,x\,lainnya\). Hitung \(P({X_1} < {X_2}|{X_1} < 2{X_2})\) .
3/4 4/7 2/3 1/5 3/8
PEMBAHASAN
Diketahui \(f(x) = \exp ( – x)\) Rumus \(f({x_1},{x_2}) = f({x_1})f({x_2})\)
\(f({x_1},{x_2}) = {e^{ – {x_1}}}{e^{ – {x_2}}}\,,\,0 < {x_1},{x_2} < \infty \) Step 1
\(P({X_1} < {X_2}|{X_1} < 2{X_2}) = \frac{{P({X_1} < {X_2})}}{{P({X_1} < 2{X_2})}}\) Step 2 \(P({X_1} < {X_2}) = \int\limits_0^\infty {\int\limits_0^{{x_2}} {{e^{ – {x_1}}}{e^{ – {x_2}}}} } \,d{x_1}d{x_2}\)
\(P({X_1} < {X_2}) = \int\limits_0^\infty {{e^{ – {x_2}}}\left( { – 1} \right)\left( {{e^{ – {x_2}}} – 1} \right)} d{x_2}\)
\(P({X_1} < {X_2}) = \int\limits_0^\infty {\left( {{e^{ – {x_2}}} – {e^{ – 2{x_2}}}} \right)} d{x_2}\)
\(P({X_1} < {X_2}) = \left( { – 1(0 – 1)} \right) – \left( { – \frac{1}{2}(0 – 1)} \right)\)
\(P({X_1} < {X_2}) = 1 – \frac{1}{2}\)
\(P({X_1} < {X_2}) = \frac{1}{2}\) \(P({X_1} < 2{X_2}) = \int\limits_0^\infty {\int\limits_0^{2{x_2}} {{e^{ – {x_1}}}{e^{ – {x_2}}}} } \,d{x_1}d{x_2}\)
\(P({X_1} < 2{X_2}) = \int\limits_0^\infty {{e^{ – {x_2}}}\left( { – 1} \right)\left( {{e^{ – 2{x_2}}} – 1} \right)} d{x_2}\)
\(P({X_1} < 2{X_2}) = \int\limits_0^\infty {\left( {{e^{ – {x_2}}} – {e^{ – 3{x_2}}}} \right)} d{x_2}\)
\(P({X_1} < 2{X_2}) = \left( { – 1(0 – 1)} \right) – \left( { – \frac{1}{3}(0 – 1)} \right)\)
\(P({X_1} < 2{X_2}) = 1 – \frac{1}{3}\)
\(P({X_1} < 2{X_2}) = \frac{2}{3}\) Step 3 \(P({X_1} < {X_2}|{X_1} < 2{X_2}) = \frac{{\left( {\frac{1}{2}} \right)}}{{\left( {\frac{2}{3}} \right)}}\)
\(P({X_1} < {X_2}|{X_1} < 2{X_2}) = \frac{3}{4}\) Jawaban a. 3/4
Optimized by Seraphinite Accelerator
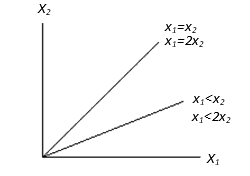\(P({X_1} < {X_2}|{X_1} < 2{X_2}) = \frac{{P({X_1} < {X_2})}}{{P({X_1} < 2{X_2})}}\)