Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | A20 – Probabilitas dan Statistika |
| Periode Ujian | : | Juni 2016 |
| Nomor Soal | : | 9 |
SOAL
Seorang perusahaan asuransi memprediksi bahwa waktu hidup Joko berdistribusi uniform dengan interval [0,5] dan waktu hidup Amir berdistribusi uniform dengan interval [0,10]. Perusahaan asuransi mengasumsikan bahwa waktu hidup antara satu individu dengan individu yang lain ialah peubah acak yang saling bebas. Berapa peluang bahwa Joko meninggal terlebih dahulu daripada Amir?
- 1/4
- 1/3
- 1/2
- 2/3
- 3/4
PEMBAHASAN
| Misalkan | J ialah waktu hidup Joko
A ialah waktu hidup Amir
J ~ Uniform [0,5]
A ~ Uniform [0,10] |
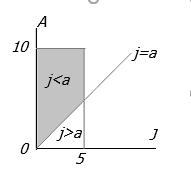
| Step 1 |  \(P(J \le A) = \,1\, – \,P(J > A)\)
\(P(J > A) = \int\limits_0^5 {\int\limits_0^j {\left( {\frac{1}{{50}}} \right)dadj} } \)
\(P(J > A) = \int\limits_0^5 {\left( {\frac{j}{{50}}} \right)dj} \)
\(P(J > A) = \left( {\frac{{{j^2}}}{{100}}} \right)\left| {_0^5} \right.\)
\(P(J > A) = \left( {\frac{{25}}{{100}}} \right)\)
\(P(J > A) = \frac{1}{4}\)
\(P(J \le A) = \,1\, – \,P(J > A)\)
\(P(J > A) = \int\limits_0^5 {\int\limits_0^j {\left( {\frac{1}{{50}}} \right)dadj} } \)
\(P(J > A) = \int\limits_0^5 {\left( {\frac{j}{{50}}} \right)dj} \)
\(P(J > A) = \left( {\frac{{{j^2}}}{{100}}} \right)\left| {_0^5} \right.\)
\(P(J > A) = \left( {\frac{{25}}{{100}}} \right)\)
\(P(J > A) = \frac{1}{4}\) |
| Step 2 | \(P(J \le A) = \,1\, – \,\frac{1}{4}\)
\(P(J \le A) = \,\frac{3}{4}\) |
| Jawaban | e. 3/4 |



 \(P(J \le A) = \,1\, – \,P(J > A)\)
\(P(J > A) = \int\limits_0^5 {\int\limits_0^j {\left( {\frac{1}{{50}}} \right)dadj} } \)
\(P(J > A) = \int\limits_0^5 {\left( {\frac{j}{{50}}} \right)dj} \)
\(P(J > A) = \left( {\frac{{{j^2}}}{{100}}} \right)\left| {_0^5} \right.\)
\(P(J > A) = \left( {\frac{{25}}{{100}}} \right)\)
\(P(J > A) = \frac{1}{4}\)
\(P(J \le A) = \,1\, – \,P(J > A)\)
\(P(J > A) = \int\limits_0^5 {\int\limits_0^j {\left( {\frac{1}{{50}}} \right)dadj} } \)
\(P(J > A) = \int\limits_0^5 {\left( {\frac{j}{{50}}} \right)dj} \)
\(P(J > A) = \left( {\frac{{{j^2}}}{{100}}} \right)\left| {_0^5} \right.\)
\(P(J > A) = \left( {\frac{{25}}{{100}}} \right)\)
\(P(J > A) = \frac{1}{4}\)