Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Permodelan dan Teori Risiko |
| Periode Ujian | : | November 2017 |
| Nomor Soal | : | 2 |
SOAL
Diberikan data pengalaman polis asuransi kendaraan sebagai:
| | Perusahaan | Tahun 1 | Tahun 2 | Tahun 3 |
| Kerugian | A | 50.000 | 50.000 | ? |
| Jumlah kendaraan | 100 | 200 | ? |
| Kerugian | B | ? | 150.000 | 150.000 |
| Jumlah kendaraan | ? | 500 | 300 |
| Kerugian | C | 150.000 | ? | 150.000 |
| Jumlah kendaraan | 50 | ? | 150 |
Hitunglah the nonparametric empirical Bayes credibility factor, Z, untuk perusahaan C.
- kurang dari 0,2
- paling sedikit 0,2 akan tetapi kurang dari 0,4
- paling sedikit 0,4 akan tetapi kurang dari 0,6
- paling sedikit 0,6 akan tetapi kurang dari 0,8
- paling sedikit 0,8
| Diketahui | | | Perusahaan | Tahun 1 | Tahun 2 | Tahun 3 | | Kerugian | A | 50.000 | 50.000 | ? | | Jumlah kendaraan | 100 | 200 | ? | | Kerugian | B | ? | 150.000 | 150.000 | | Jumlah kendaraan | ? | 500 | 300 | | Kerugian | C | 150.000 | ? | 150.000 | | Jumlah kendaraan | 50 | ? | 150 |
|
| Rumus yang digunakan | \({Z_c} = \frac{n}{{n + \frac{{\hat v}}{{\hat a}}}}\) |
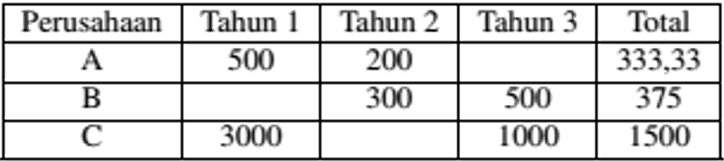
| Proses pengerjaan | Rata-rata untuk masing-masing perusahaan dan tahun adalah sebagai berikut:
\(\hat \mu \,\,\,\, = \frac{{50.000 + 50.000 + 150.000 + 150.000 + 150.000 + 150.000}}{{100 + 200 + 500 + 300 + 50 + 150}} = 538,4615\)Pembilang untuk \({\hat v}\):
\(100{(500 – 333,33)^2} + 200{(250 – 333,33)^2} + 500{(300 – 375)^2} + 300{(500 – 375)^2}\) \(+ 50{(3000 – 1500)^2} + 150{(1000 – 1500)^2} = 161.666.666\) Sehingga,
\(\hat v = \frac{{161.666.666,7}}{{(2 – 1){\rm{ }} + {\rm{ }}(2 – 1){\rm{ }} + {\rm{ }}(2 – 1)}} = 5.388.888,89\)
\(\hat a = \frac{{300{{(333,{\rm{ }}33 – 538,{\rm{ }}4615)}^2} + 800{{(375 – 538,{\rm{ }}4615)}^2} + 200{{(1500 – 538,{\rm{ }}4615)}^2}}}{{1300 – \frac{1}{{1300}}\left( {{{300}^2} + {{800}^2} + {{200}^2}} \right)}}\)
\(\hat a = 157.035,0242\) Faktor kredibilitas Bayes empirik non-parametrik untuk perusahaan C adalah:
\({Z_c} = \frac{n}{{n + \frac{{\hat v}}{{\hat a}}}} = \frac{{200}}{{200 + \frac{{5.388.888,89}}{{157.035,0242}}}} = 0,368212389\) |
| Jawaban | B. paling sedikit 0,2 akan tetapi kurang dari 0,4 |
\(\hat \mu \,\,\,\, = \frac{{50.000 + 50.000 + 150.000 + 150.000 + 150.000 + 150.000}}{{100 + 200 + 500 + 300 + 50 + 150}} = 538,4615\)