Pembahasan Soal Ujian Profesi Aktuaris
SOAL
Suatu asuransi seumur hidup pada (x) dengan manfaat 1 dengan pengembalian dari “net single premium” tanpa bunga pada saat kematian. Diberikan:
(i) \({\mu _{x + t}} = 0,01\,\,for\,t > 0\)
(ii) \(\delta = 0,02\)
Hitunglah “net single premium”
Data Polis adalah perusahaan media yang memberikan informasi mengenai perkembangan industri perasuransian dan manajemen risiko saat ini. Topik yang dibahas dari berbagai sudut pandang agar memperoleh perspektif yang lebih jelas dan lengkap. Hubungi kami melalui email untuk berdiskusi dengan kami: [email protected]
Marketing Office –
PT Data Teknologi Terintegrasi
MTH Square, GF A4/A
Jl. Letjen M.T. Haryono No. Kav 10, Jakarta Timur 13330
Phone: +62 856 856 0000
Follow Us
©
By Data Polis. All Rights Reserved.
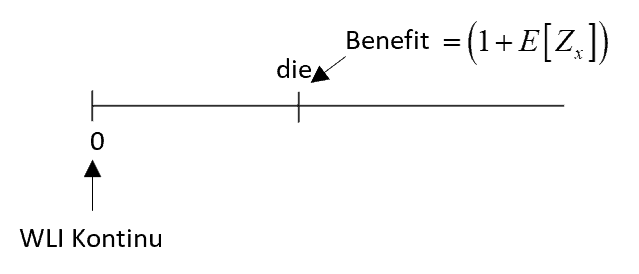\(PV\,benefit = \left( {1 + E\left[ {{Z_x}} \right]} \right){v^{{T_x}}}\,,\,{T_x} > 0\,\)
\(PV\,benefit = {Z_x}^*\)
\(E\left[ {{Z_x}^*} \right] = \left( {1 + E\left[ {{Z_x}^*} \right]} \right)E\left[ {{v^{{T_x}}}} \right]\)
