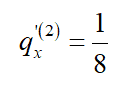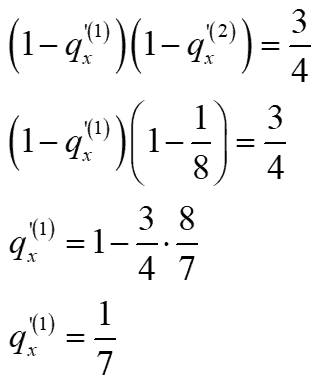Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Matematika Aktuaria |
| Periode Ujian | : | Juni 2015 |
| Nomor Soal | : | 19 |
SOAL
Untuk suatu tabel double decrement, diberikan:

- \({}_{\left. 1 \right|}q_x^{\left( 1 \right)} = \frac{1}{4}\)
- \(q_{x + 1}^{\left( 1 \right)} = \frac{1}{3}\)
Hitunglah 
- \(\frac{1}{4}\)
- \(\frac{1}{5}\)
- \(\frac{1}{6}\)
- \(\frac{1}{7}\)
- \(\frac{1}{8}\)
| Diketahui |  - \({}_{\left. 1 \right|}q_x^{\left( 1 \right)} = \frac{1}{4}\)
- \(q_{x + 1}^{\left( 1 \right)} = \frac{1}{3}\)
|
| Rumus yang digunakan | \({}_{\left. t \right|u}q_x^{\left( j \right)} = {}_tp_x^{\left( \tau \right)} \cdot {}_uq_{x + t}^{\left( j \right)}\)
\({}_tp_x^{\left( \tau \right)} = \prod\limits_{j = 1}^n {{}_tp_x^{‘\left( j \right)}} = \prod\limits_{j = 1}^n {\left( {1 – {}_tq_x^{‘\left( j \right)}} \right)} \) |
| Proses pengerjaan | \({}_{\left. 1 \right|}q_x^{\left( 1 \right)} = p_x^{\left( \tau \right)} \cdot q_{x + 1}^{\left( 1 \right)}\)
\(\frac{1}{4} = \frac{1}{3}p_x^{\left( \tau \right)}\)
\(p_x^{\left( \tau \right)} = \frac{3}{4}\)
 |
| Jawaban | d. \(\frac{1}{7}\) |

![]()