Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Metoda Statistika |
| Periode Ujian | : | November 2016 |
| Nomor Soal | : | 19 |
SOAL
Misalkan anda melakukan smoothing deret waktu \({y_t}\) menggunakan metode exponential smoothing 2-parameter dari Holt:
 Hitunglah forecast 2-periode \({\widehat y_{2000}}\) dengan terlebih dahulu melengkapi tabel di atas dengan deret exponential 2-parameter dari Holt
Hitunglah forecast 2-periode \({\widehat y_{2000}}\) dengan terlebih dahulu melengkapi tabel di atas dengan deret exponential 2-parameter dari Holt
- Lebih kecil dari 166
- Paling sedikit 166, tetapi lebih sedikit 172
- Paling sedikit 172, tetapi lebih kecil dari 176
- Paling sedikit 176, tetapi lebih kecil dari 180
- Paling sedikit 180
| Diketahui | smoothing deret waktu \({y_t}\) menggunakan metode exponential smoothing 2-parameter dari Holt 
|
| Rumus yang digunakan | \({{\tilde y}_t} = \alpha {y_t} + \left( {1 – \alpha } \right)\left( {{{\tilde y}_{t – 1}} + {r_{t – 1}}} \right)\)
\({r_t} = \gamma \left( {{{\tilde y}_t} – {{\tilde y}_{t – 1}}} \right) + (1 – \gamma ){r_{t – 1}}\)
\({\widehat y_{T + l}} = {{\tilde y}_T} + l{r_T}\) |
| Proses pengerjaan | Mencari nilai dari \(\alpha \) dan \(\gamma \)
\({{\tilde y}_{1996}} = \alpha {y_{1996}} + \left( {1 – \alpha } \right)\left( {{{\tilde y}_{1995}} + {r_{1995}}} \right)\)
\(\Leftrightarrow 131.7 = 135\alpha + \left( {1 – \alpha } \right)\left( {117.5 + 12} \right)\)
\(\Leftrightarrow 131.7 = 135\alpha + 129.5 – 129.5\alpha \)
\(\Leftrightarrow 5.5\alpha = 2.2\)
\(\Leftrightarrow \alpha = \frac{{2.2}}{{5.5}} = 0.4\)
\({r_{1996}} = \gamma \left( {{{\tilde y}_{1996}} – {{\tilde y}_{1995}}} \right) + (1 – \gamma ){r_{1995}}\)
\(\Leftrightarrow 13 = \gamma \left( {131.7 – 117.5} \right) + (1 – \gamma )12\)
\(\Leftrightarrow 13 = 12 + 2.2\gamma \)
\(\Leftrightarrow \gamma = \frac{{13 – 12}}{{2.2}} = \frac{5}{{11}}\) maka
\({{\tilde y}_{1998}} = \alpha {y_{1998}} + \left( {1 – \alpha } \right)\left( {{{\tilde y}_{1997}} + {r_{1997}}} \right)\)
\(= \left( {0.4} \right)\left( {146.6} \right) + \left( {1 – 0.4} \right)\left( {146.29 + 14.36} \right)\)
\(= 155.03\)
dan
\({r_{1998}} = \gamma \left( {{{\tilde y}_{1998}} – {{\tilde y}_{1997}}} \right) + (1 – \gamma ){r_{1997}}\)
\(= \left( {\frac{5}{{11}}} \right)\left( {155.03 – 146.6} \right) + (1 – \frac{5}{{11}})14.36\)
\(= 11.66\)
\({\widehat y_{1998 + 2}} = {\widehat y_{1998}} + 2{r_{1998}}\)
\(= 155.03 + 2(11.66)\)
\(= 178.359\) |
| Jawaban | d. Paling sedikit 176, tetapi lebih kecil dari 180 |
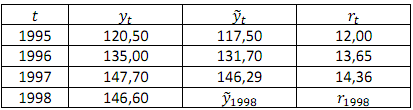 Hitunglah forecast 2-periode \({\widehat y_{2000}}\) dengan terlebih dahulu melengkapi tabel di atas dengan deret exponential 2-parameter dari Holt
Hitunglah forecast 2-periode \({\widehat y_{2000}}\) dengan terlebih dahulu melengkapi tabel di atas dengan deret exponential 2-parameter dari Holt

