Pembahasan Soal Ujian Profesi Aktuaris
| Institusi |
: |
Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian |
: |
Metoda Statistika |
| Periode Ujian |
: |
November 2016 |
| Nomor Soal |
: |
10 |
SOAL
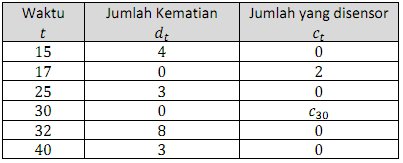
Sebuah studi mortalita dilakukan atas pengamatan terhadap 50 peserta dimulai dari waktu 0, diketahui
\(\widehat S(35){\rm{ }}\) adalah estimasi produk limit dari \(S(35)\)
\(\widehat V[\widehat S(35)]\) adalah estimasi variasi dari \(\widehat S(35)\) menggunakan formula Greenwood
\(\frac{{\widehat V[\widehat S(35)]}}{{{{\left[ {\widehat S(35)} \right]}^2}}} = 0.012452\)
Hitunglah \({c_{30}},\) jumlah yang disensor pada waktu \(t = 30\)
- 6
- 7
- 8
- 9
- 10
| Diketahui |
\(\frac{{\widehat V[\widehat S(35)]}}{{{{\left[ {\widehat S(35)} \right]}^2}}} = 0.012452\)
\(\widehat V[\widehat S(35)]\) adalah estimasi variasi dari \(\widehat S(35)\) menggunakan formula Greenwood |
| Rumus yang digunakan |
\(\widehat V[\widehat S(t)] = {[\widehat S(t)]^2}.\sum\limits_{j = 1}^k {\left( {\frac{{{d_j}}}{{{r_j}({r_j} – {d_j})}}} \right)} \) |
| Proses pengerjaan |
\(\widehat V[\widehat S(35)] = {[\widehat S(35)]^2}.\sum\limits_{j = 1}^3 {\left( {\frac{{{d_j}}}{{{r_j}({r_j} – {d_j})}}} \right)} \)
\(\Leftrightarrow \sum\limits_{j = 1}^3 {\left( {\frac{{{d_j}}}{{{r_j}({r_j} – {d_j})}}} \right)} = \frac{{\widehat V[\widehat S(35)]}}{{{{[\widehat S(35)]}^2}}}\)
\(\Leftrightarrow \left( {\frac{4}{{50(46)}}} \right) + \left( {\frac{3}{{44(41)}}} \right) + \left( {\frac{8}{{(41 – c)(33 – c)}}} \right) = 0.012452\)
\(\Leftrightarrow 1353 – 74c + {c^2} = 884\)
\(\Leftrightarrow 469 – 74c + {c^2} = 0\)
sehingga,
\({c_{1,2}} = \frac{{74 \pm \sqrt {{{74}^2} – 4(1)(469)} }}{{2(1)}} = 7\) |
| Jawaban |
b. 7 |
