Pembahasan Soal Ujian Profesi Aktuaris
SOAL
Dari suatu sampel acak persentil ke-20 ialah 18,25 dan persentil ke-80 ialah 35,8. Hitung estimasi dari parameter suatu distribusi log-normal menggunakan metode persentile-matching dan gunakan estimasi tersebut untuk menghitung peluang mengamati suatu nilai melebihi 30.
- 0,2176
- 0,1174
- 0,0008
- 0,3446
- 0,2572
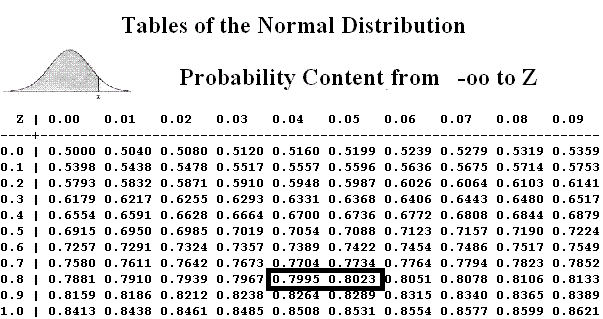
| Diketahui | \(F(18,25) = \Phi \left( {\frac{{\ln 18,25 – \mu }}{\sigma }} \right) = 0,2\) \(F(35,8) = \Phi \left( {\frac{{\ln 35,8 – \mu }}{\sigma }} \right) = 0,8\) |
| Rumus | Standard Normal Distribution, \(\Pr \left( {Z < z} \right) = \Phi \left( {\frac{{\ln z – \mu }}{\sigma }} \right)\) |
| Step 1 |  Pada tabel distribusi normal diatas, 0,8 berada diantara z=0,84 dan z=0,85. Dengan rumus interpolasi, Maka 0,8 berada tepat saat z=0,842 |
| Step 2 |
|
| |
| \(\frac{{\ln 35,8 – 3,241}}{\sigma } = 0,842\) \(\sigma = 0,4001756454\) \(\sigma \cong 0,4\) | |
| Maka | \(\Pr \left( {Z > 30} \right) = 1 – \Pr (Z < 30)\) \(\Pr \left( {Z > 30} \right) = 1 – \Phi \left( {\frac{{\ln 30 – 3,241}}{{0,4}}} \right)\) \(\Pr \left( {Z > 30} \right) = 1 – \Phi \left( {0,4} \right)\) \(\Pr \left( {Z > 30} \right) = 1 – 0,6554\) \(\Pr \left( {Z > 30} \right) = 0,3446\) |
| Jawaban | d. 0,3446 |