Pembahasan Ujian PAI: A60 - No. 7 - Mei 2018

Pembahasan Soal Ujian Profesi Aktuaris

Institusi	:	Persatuan Aktuaris Indonesia (PAI)
Mata Ujian	:	Matematika Aktuaria
Periode Ujian	:	Mei 2018
Nomor Soal	:	7

SOAL

Diberikan sebuah fungsi survival dari seorang bayi yang baru lahir :

\({S_0}\left( s \right) = \left\{ \begin{array}{l} 1 – \frac{x}{{250}},\,\,0 \le x \le 40\\ 1 – {\left( {\frac{x}{{100}}} \right)^2},\,\,40 \le x \le 100 \end{array} \right.\)

Hitunglah probabilitas seseorang yang berumur 25 tahun akan meninggal dalam 30 tahun.

0,210
0,215
0,220
0,225
0,230

Kunci Jawaban & Pembahasan

Diketahui	\({S_0}\left( s \right) = \left\{ \begin{array}{l} 1 – \frac{x}{{250}},\,\,0 \le x \le 40\\ 1 – {\left( {\frac{x}{{100}}} \right)^2},\,\,40 \le x \le 100 \end{array} \right.\)
Ditanya	\(_{30}{q_{25}}\)
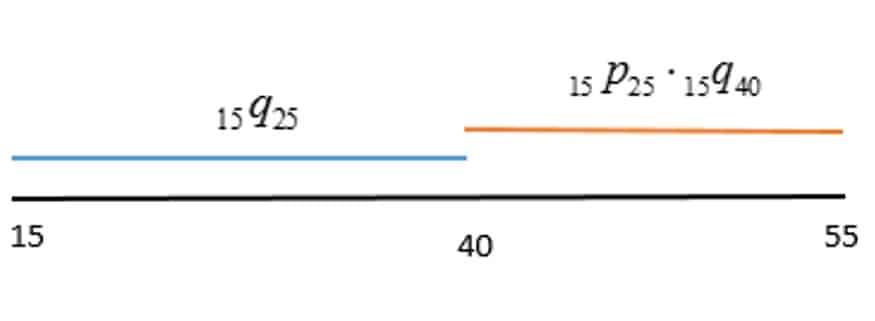
Step 1	\(_{30}{q_{25}} = {\,_{15}}{q_{25}} + {\,_{15}}{p_{25}} \cdot {\,_{15}}{q_{40}}\) ………(*)
Step 2	\(_{15}{p_{25}} = \frac{{S\left( {40} \right)}}{{S\left( {25} \right)}} = \frac{{1 – {{\left( {\frac{{40}}{{100}}} \right)}^2}}}{{1 – \left( {\frac{{25}}{{250}}} \right)}} = \frac{{0,84}}{{0,9}} = 0,9333\) \(_{15}{q_{25}} = 1{ – _{15}}{p_{25}} = 1 – 0,9333 = 0,0667\) \(_{15}{p_{40}} = \frac{{S\left( {55} \right)}}{{S\left( {40} \right)}} = \frac{{1 – {{\left( {\frac{{55}}{{100}}} \right)}^2}}}{{1 – {{\left( {\frac{{40}}{{100}}} \right)}^2}}} = \frac{{0,6975}}{{0,84}} = 0,830357142\) \(_{15}{q_{40}} = 1 – 0,830357142 = 0,169642857\)
Step 3	(*) \(_{30}{q_{25}} = {\,_{15}}{q_{25}} + {\,_{15}}{p_{25}} \cdot {\,_{15}}{q_{40}}\) \(= 0,0667 + 0,9333 \cdot 0,169642857\) \(= 0,225\)
Jawaban	d. 0,225

Pembahasan Ujian PAI: A60 – No. 7 – Mei 2018