Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Matematika Aktuaria |
| Periode Ujian | : | November 2017 |
| Nomor Soal | : | 10 |
SOAL
Suatu pembayaran dilakukan sebesar 10 di akhir minggu untuk memenuhi kebutuhan pembelian detergen. Kegunaan detergen adalah variabel, “the week of exhaustion of supply” adalah variabel acak K
| k | Pr(K=k) |
| 1 | 0,20 |
| 2 | 0,30 |
| 3 | 0,20 |
| 4 | 0,15 |
| 5 | 0,15 |
Misalkan \(Z = 10{v^K}\) menyatakan “present value” dari pembayaran variabel acak. Dengan asumsi bunga \(i = 0,01\), “effective per week”
Hitunglah “median” dari Z
- 9,706
- 10,706
- 11,706
- 12,706
- 13,706
| Diketahui | \(K\) ialah variabel acak kekurangan detergen (satuan minggu)
\(Z\) ialah nilai sekarang dari pembayaran variabel acak
\(P({K_x} = k)\) ialah probabilitas kekurangan detergen pada minggu ke-k |
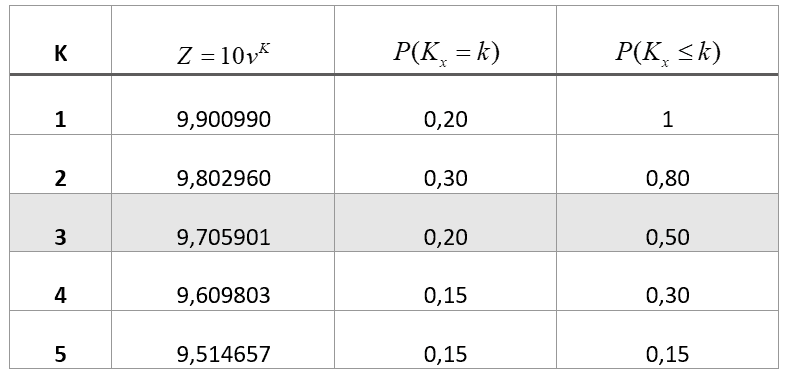
| Step 1 | \(Z = 10{v^K}\)
\(k = 1\)
\(Z = \frac{{10}}{{1,01}} = 9,900990\)
\(k = 2\)
\(Z = \frac{{10}}{{{{1,01}^2}}} = 9,802960\)
\(k = 3\)
\(Z = \frac{{10}}{{{{1,01}^3}}} = 9,705901\)
\(k = 4\)
\(Z = \frac{{10}}{{{{1,01}^4}}} = 9,609803\)
\(k = 5\)
\(Z = \frac{{10}}{{{{1,01}^5}}} = 9,514657\) |
| Step 2 | \(P({K_x} \le k)\)
\(P({K_x} \le 1) = 1 – P({K_x} = 0) = 1 – 0 = 1\)
\(P({K_x} \le 1) = 1 – \left( {P({K_x} = 0) + P({K_x} = 1)} \right) = 1 – 0,2 = 0,8\)
\(P({K_x} \le 1) = 1 – \left( {P({K_x} = 0) + P({K_x} = 1) + P({K_x} = 2)} \right) = 1 – 0,5 = 0,5\) |
| 
Sehingga, median dari Z ialah \(9,705901\,\, \cong \,9,706\) |
| Jawaban | a. 9,706 |