Dalam matematika keuangan, pertumbuhan uang biasanya diukur dengan menggunakan konsep bunga. Bunga adalah imbal hasil yang diterima dari suatu investasi atau pinjaman. Jika seseorang menabung di bank, ia akan menerima bunga atas tabungannya. Sebaliknya, jika seseorang meminjam uang dari bank, ia harus membayar bunga atas pinjamannya.
Sederhananya, bunga yang dimaksud sebagai kompensasi atas peminjaman modal kepada pemberi pinjaman modal. Bunga dan modal hampir selalu dinyatakan dalam bentuk uang. Konsep suatu investasi atau pinjaman ialah sebagai berikut:
- Sejumlah uang atau modal (Principal) diinvestasikan untuk jangka waktu tertentu
- Pada akhir periode investasi, nilai akumulasi (Accumulated Value) dikembalikan
- Selisih antara Nilai Akumulasi dengan Pokok adalah Bunga yang Diperoleh
Fungsi Akumulasi / Accumulation Value: \(a\left( t \right)\) dimana t ialah jumlah tahun investasi (t ≥ 0)
Fungsi Nilai / Amount Function: \(A\left( t \right) = k.\;a\left( t \right)\) yaitu Nilai Akumulasi atas pertumbuhan Pokok Pinjaman dalam tahun
Bunga yang diperoleh selama nth periode: \(I{\;_n}\; = \;A\left( n \right)\; – \;A\left( {n\; – \;1} \right)\) yaitu selisih antara Nilai Akumulasi pada akhir periode dan Nilai Akumulasi pada awal periode.
Bunga
The Effective Rate of Interest atau tingkat bunga efektif dikonotasikan sebagai ” didefinisikan sebagai rasio jumlah Bunga yang diperoleh selama periode tersebut terhadap Akumulasi Nilai pada awal periode.
\({i_n} = \frac{{A\left( n \right) – A\left( {n – 1} \right)}}{{A\left( {n – 1} \right)}} = \frac{{{I_n}}}{{A\left( {n – 1} \right)}},\;for\;integral\;n \ge 1\)Bunga Sederhana/ Simple Interest
Jenis bunga ini mengasumsikan bahwa bunga bertambah selama t tahun dan kemudian diinvestasikan kembali selama s tahun di mana s< 1. Bunga yang diperoleh setiap tahun atas investasi sebesar 1 menjadi konstan pada \(i\) dan \(a\left( 0 \right) = 1,\;\;a\left( 1 \right)\; = \;1\; + \;i\)
Bunga sederhana TIDAK menginvestasikan kembali bunga yang didapat.
Ini adalah fungsi akumulasi linier, \(a\left( t \right) = 1 + it\), untuk integral t ≥ 0
Bunga Majemuk/ Compound Interest
Jenis bunga ini membiarkan bunga yang diperoleh setiap tahun atas investasi sebesar 1 menjadi konstan pada \(i\) dan \(a\left( 0 \right) = 1,\;\;a\left( 1 \right)\; = \;1\; + \;i\)
Bunga ini menginvestasikan kembali bunga yang didapat unyuk mendapatkan bunga tambahan.
Ini merupakan fungsi akumulasi eksponensial \(a\left( t \right)\; = \;{\left( {1\; + \;i} \right)^t}\) untuk integral t ≥ 0. Bunga majemuk menghasilkan akumulasi yang lebih besar daripada bunga sederhana ketika t> 1
Berikut ilustrasi Nilai Akumulasi dengan 2 jenis bunga:
Asumsi,
Pokok Pinjaman \(\left( {{\rm{}}k{\rm{}}} \right)\)= 100
Tingkat Bunga Efektif \(\left( {{\rm{}}i{\rm{}}} \right) = 30{\rm{\% }}\)
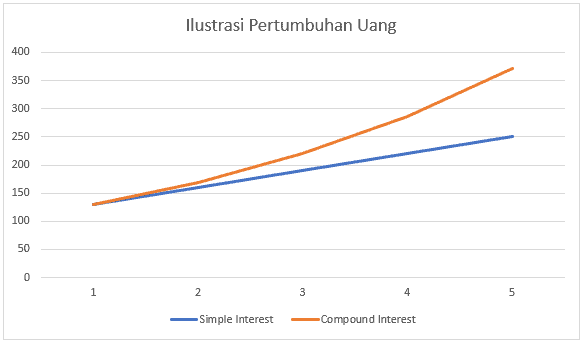
Source: Theory of Interest (Second Edition), 1991, by Kellison, S.G.


