Pembahasan Soal Ujian Profesi Aktuaris
| Institusi | : | Persatuan Aktuaris Indonesia (PAI) |
| Mata Ujian | : | Metoda Statistika |
| Periode Ujian | : | Mei 2017 |
| Nomor Soal | : | 8 |
SOAL
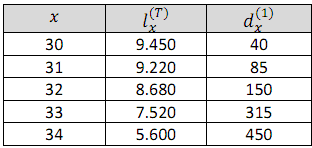
Pada sebuah model double decrement, diperoleh informasi sebagai berikut:

Hitunglah probabilitas bahwa seseorang yang berumur 30 tahun akan berkurang dalam 3 tahun karena decrement ke-2.
- 0.165
- 0.170
- 0.175
- 0.18
- 0.185
| Diketahui |  |
| Rumus yang digunakan | Untuk double decrement
\(l_{x + 1}^{(\tau )} = l_x^{(\tau )} – d_x^{(1)} – d_x^{(2)}\)
\(_nq_x^{(j)} = \frac{{\sum\limits_{i = 0}^{n – 1} {d_{x + i}^{(j)}} }}{{l_x^{(\tau )}}}\) |
| Proses pengerjaan | Bedasarkan \(l_{x + 1}^{(\tau )} = l_x^{(\tau )} – d_x^{(1)} – d_x^{(2)}\) diperoleh tabel| x | \(l_x^{(\tau )}\) | \(d_x^{(1)}\) | \(d_x^{(2)}\) | | 30 | 9450 | 40 | 190 | | 31 | 9220 | 85 | 455 | | 32 | 8680 | 150 | 1010 | | 33 | 7520 | 315 | 1605 | | 34 | 5600 | 450 | |
\(_3q_{30}^{(j)} = \frac{{\sum\limits_{i = 0}^{n – 1} {d_{30 + i}^{(j)}} }}{{l_x^{(\tau )}}} = \frac{{190 + 455 + 1010}}{{9450}} = 0.17513\) |
| Jawaban | c. 0.175 |